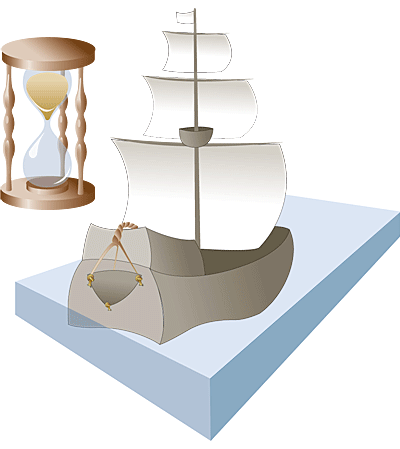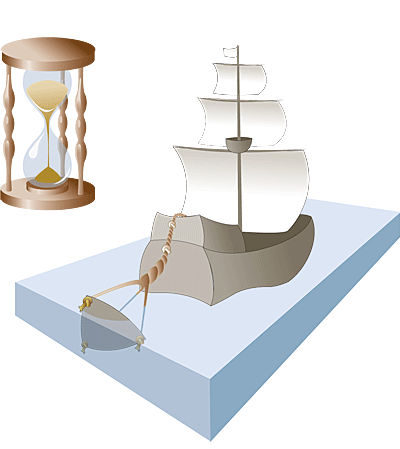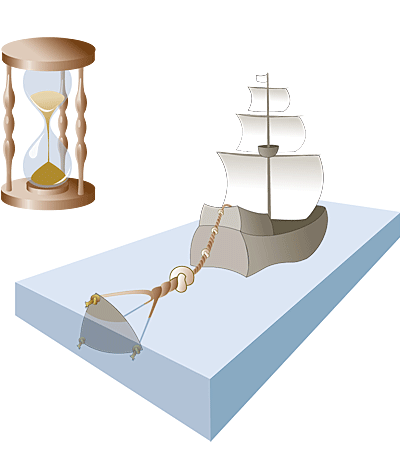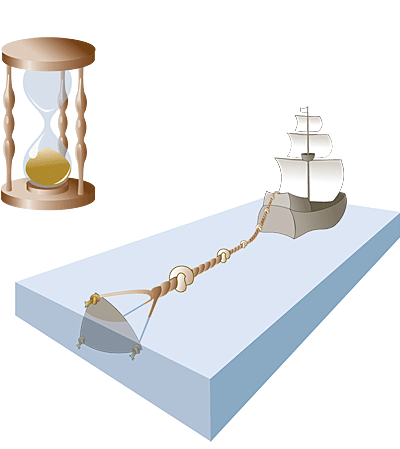
“节”这个单位最早可以追溯到16世纪,此时世界正在经历大航海时代,各国使用的都是风帆船。没有卫星定位,在茫茫大海上也找不到任何的参照物。该怎么计算船的航速呢?当时欧洲的水手们就想了一个办法,用沙漏、绳子外加浮标来确定一艘船的航速。

具体做法是,用绳索绑上浮标抛到大海中,船航行时,一段一段的往下放绳子,每一段打上一个绳结,结与结之间是等长的。抛下浮标后,就开始用沙漏计时,通过放下去多少结绳子再除以沙漏计下的时间就可以算出船速了。

你可能觉得这种测算航速的方法太过原始,但是其实是很准确的。沙漏的容积可以算出来,流速也是可以确定的,当时欧洲制造玻璃的工艺已经非常娴熟,所以这样算出的速度也是比较准确的。
问题出在不统一上,各国水手打的绳结长度不一样,荷兰、英国、西班牙的都不一样,这就给海上贸易以及航线的测定带来了很大麻烦。要想定义速度,就先要把绳结的长度给统一了。
怎么确定呢?这就要用到地理学的知识了。
在15世纪的时候,人们已经猜测地球是一个球体。这个猜想在1522年麦哲伦船队完成环球航行回到西班牙以后得到了确认,至此“地球是一个球体”基本成为了一个定理。

欧洲的数学家、天文学家和物理学家一直都有一个执念,他们好多依旧信仰上帝,认为上帝创造的地球伊甸园一定是完美的几何球形。有了这个共识之后,就可以定义1海里有多长了。
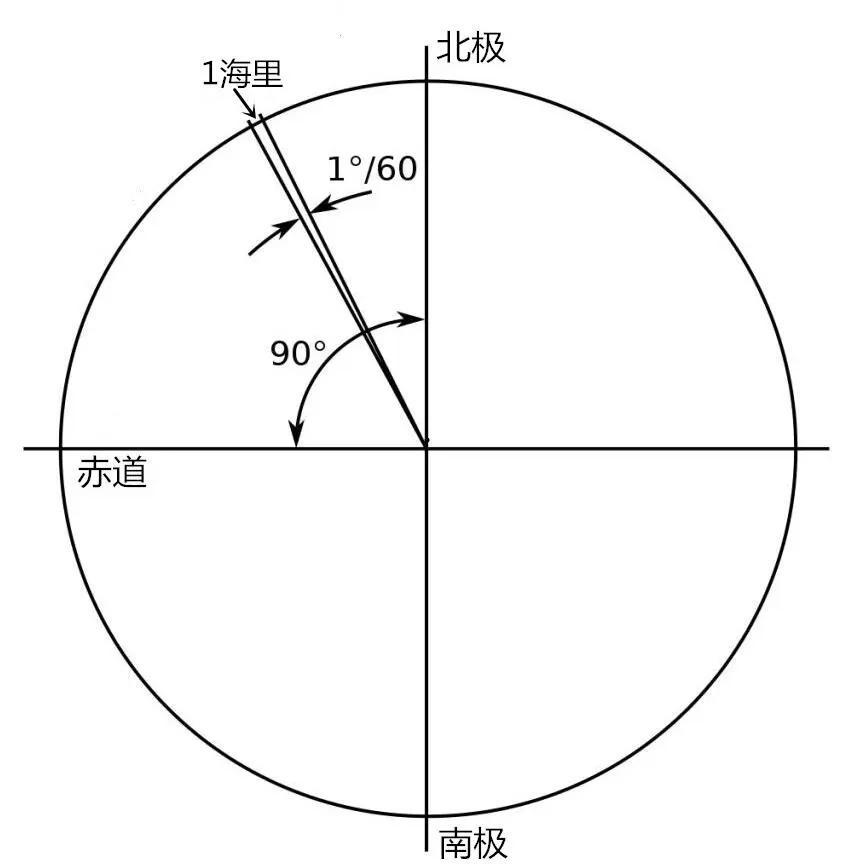
这里有一个数学知识,那就是在一个球形上画出一个圆,半径最大的那个必然经过球心。于是当时的人们就定义,过圆心最大的圆,夹角一分所对应的大圆弧长就等于1海里。这里的一分角度是1/60度,一个圆有360度。相当于把地球最大圆的周长分成了21600份,每份就是1海里。
那么问题来了,地球直径有多少呢?当时有人可以算出来吗?
这不是什么难题,只要两根木棍就可以。春分日开始后,太阳直射点向北移,当太阳直射地球的时候,这时我们可以近似认为直射点的阳光延长线是穿过球心的。在地面插上一根木棍,然后在离木棍很远的北方也插一根木棍,二者距离记作D,当南面的木棍影子消失不见的时候,就说明太阳光直射到这里了。

然后量出背面木棍上的影子长度,用影子长度与木棍长度求出阳光与棍子之间的夹角,依据平行线同位角相等,就知道了D这段距离对应的地球大圆角度,用360度除以这个角度,乘上D得到的就是地球的大圆弧长了。
知道大圆弧长以后,海里的长度就出来了。只不过当时的1海里并不是如今的1.852公里,因为“公里”这个单位要到十八世纪才由法国人确立,到十九世纪七十年代才被确立为国际单位。所以当时的1海里,在英国人看来就是0.621英里,一节就是0.621英里/小时。

后来,随着物理学和天文学的发展,人们意识到了,原来地球不是完美的球形,用这种方式来计算航海距离和速度是有误差的。纬度低的地方,一分对应的弧度要长,而纬度高的地方要短,所以低纬度国家一节的速度是要大于1.852公里/小时的。

当然,如果纯粹按照数学来定义的话,那就乱套了,所以后来国际规定就以1.852公里来代表1海里,这是子午线对应一分角的弧长。虽然还是不精确,但是它已经成为了一个约定俗成的单位。
1海里的长度明确了,那么一节的速度就很简单了,节与公里/小时的换算只要乘上一个1.852系数就行。比如某航母的最大航速是30节,那么实际上它的速度是55.6公里/小时。

因为卫星定位系统的出现,现在海上航行不用节来表示航速也可以,这个单位属于一个老单位,就和中国以前的“半斤八两”一样,用起来不怎么方便。可是在古代,这个单位是非常适合航海的,只要一个六分仪外加一个怀表就能测算出帆船的航速。“半斤八两”也是一样,一斤16两就是2的4次方两,这样设定是为了在没有秤的情况下,用体积大小就能更好的分配谷物和银两,折半就可以。