
1、什么是环形跑道问题?
环形跑道问题特殊场地行程问题之一。是多人(一般至少两人)多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析。
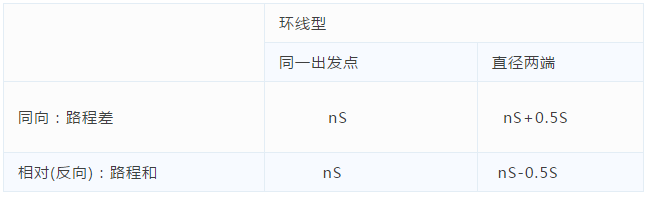
2、在做出线段图后,反复的在每一段路程上利用:
路程和=相遇时间×速度和
路程差=追及时间×速度差
3、解环形跑道问题的一般方法:
环形跑道问题,从同一地点出发,如果是相向而行,则每合走一圈相遇一次;如果是同向而行,则每追上一圈相遇一次.这个等量关系往往成为我们解决问题的关键。
例1:
环形跑道的周长是800米,甲、乙两名运动员同时顺时针自起点出发,甲的速度是每分钟400米,乙的速度是每分钟375米,多少分钟后两人第一次相遇?甲、乙两名运动员各跑了多少米?甲、乙两名运动员各跑了多少圈?
思路点拨: 在环形跑道上,这是一道封闭路线上的追及问题,第一次相遇时,快的应比慢的多跑一圈,环形跑道的周长就是追及路程,已知了两人的速度,追及时间即是两人相遇的时间。
400-375=25(米)
800÷25=32(分钟)
甲:400×32=12800(米)
乙:375×32=12000(米)
甲:12800÷800=16(圈)
乙:16-1=15(圈)
例2:
幸福村小学有一条200米长的环形跑道,冬冬和晶晶同时从起跑线起跑,冬冬每秒钟跑6米,晶晶每秒钟跑4米,问冬冬第一次追上晶晶时两人各跑了多少米,第2次追上晶晶时两人各跑了多少圈?
解:
①冬冬第一次追上晶晶所需要的时间:200÷(6-4)=100(秒)
②冬冬第一次追上晶晶时他所跑的路程应为:6×100=600(米)
③晶晶第一次被追上时所跑的路程:4×100=400(米)
④冬冬第二次追上晶晶时所跑的圈数:(600×2)÷200=6(圈)
⑤晶晶第2次被追上时所跑的圈数:(400×2)÷200=4(圈)
例3:
成才小学有一条200米长的环形跑道,包包昊昊同时从起跑线起跑包包每秒钟跑6米,昊昊每秒钟跑4米,问包包第一次追上昊昊时两人各跑了多少米?第一次追上昊昊时两人各跑了多少圈?
分析:
1、包包和昊昊同时从起跑线起跑
2、包包追上昊昊多跑一周200米,需用时200÷(6-4)=100(秒)
因此,追上昊昊时包包跑了6×100=600米,600÷200=3(圈),
昊昊跑了4×100=400米,400÷200=2(圈)
例4:
一个圆的周长为1.26米,两只蚂蚁从一条直径的两端同时出发沿圆周相向爬行.这两只蚂蚁每秒分别爬行5.5厘米和3.5厘米.它们每爬行1秒,3秒,5秒…(连续的奇数),就调头爬行。那么,它们相遇时已爬行的时间是多少秒?
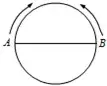
答案解析:
这道题难在蚂蚁爬行的方向不断地发生变化,那么如果这两只蚂蚁都不调头爬行,相遇时它们已经爬行了多长时间呢?
非常简单,由于半圆周长为:1.26÷2=0.63米=63厘米,所以可列式为:1.26÷2÷(5.5+3.5)=7(秒);我们发现蚂蚁爬行方向的变化是有规律可循的,它们每爬行1秒、3秒、5秒、…(连续的奇数)就调头爬行。
每只蚂蚁先向前爬1秒,然后调头爬3秒,再调头爬5秒,这时相当于在向前爬1秒的基础上又向前爬行了2秒;同理,接着向后爬7秒,再向前爬9秒,再向后爬11秒,再向前爬13秒,这就相当于一共向前爬行了1+2+2+2=7(秒),正好相遇。
解:
它们相遇时应是行了半个圆周,半个圆周长为:
1.26÷2=0.63(米)=63(厘米);
如不调头,它们相遇时间为:
63÷(3.5+5.5)=7(秒);
根据它们调头再返回的规律可知:
由于1-3+5-7+9-11+13=7(秒),
所以13+11+9+7+5+3+1=49(秒)相遇.
答:它们相遇时已爬行的时间是49秒。
点评:完成本题关健是发现蚂蚁爬行方向的变化是有规律可循。