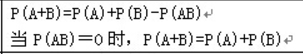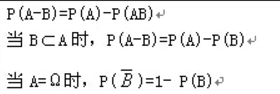概率虽然简单,但是也不能“轻敌”,据统计,每年概率部分失分率不低,大家一定要注意打好基础。下面我为大家总结概率知识点,我们一起来梳理梳理。
条件概率:设A与B为两事件,且P(A)>0,称P(B|A)=P(AB)/P(A)为在事件A发生的条件下事件B发生的条件概率。
事件独立性:设A,B两事件满足等式P(AB)=P(A)P(B),则称A与B相互独立。
加法公式:
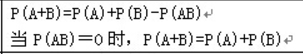
加法公式
减法公式:
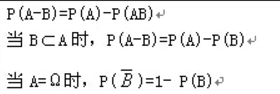
减法公式
乘法公式:

乘法公式
全概率公式:

全概率公式
贝叶斯公式:

贝叶斯公式
注:(1)概率计算中常要结合对偶律应用性质;
(2)计算相互独立事件的概率时,常将事件之间的“并”或“差”转化成“交”来计算。
题型一:加法公式的应用
例1:设A,B,C是三个随机事件,且P(A)=P(B)=P(C)=1/4,P(AB)=P(BC)=0,P(AC)=1/8,则A,B,C至少有一个发生的概率是多少。
解题思路:“至少有一个发生”的概率相当于求A,B,C并集的概率,于是可以用概率的加法公式。
解:利用加法公式进行求解

题型二:全概率公式和贝叶斯公式的应用
例2:有两个盒子,第一个盒中装有2个红球,1个白球,第二盒中装一个红球,一个白球。现从两盒中各任取一球放在一起,再从中取一球,问:
(1)这个球是红球的概率;
(2)若发现这个球是红球,问第一盒中取出的球是红球的概率。
解题思路:本题主要是全概率公式和贝叶斯公式的应用。
解:利用全概率公式和贝叶斯公式进行求解

总结:全概率公式和贝叶斯公式的应用首先要对问题中所涉及的事件进行假设,其次要确定全集的完备事件组。

 手机版
手机版